- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- Donate
Comparing Fractions Worksheet

Welcome to our Comparing Fractions Worksheets page.
Here you will find our selection of worksheets to help you to learn and practice comparing two or more fractions.
Our worksheets introduce the concept of comparing fractions in a visual way using shapes to aid understanding.
Quicklinks to...
- How to Compare Fractions?
- All Comparing Fractions Worksheets
- Comparing Fractions Worksheets with diagrams
- Ordering Fractions Worksheets with diagrams
- Comparing Fractions Worksheets without diagrams
- Ordering Fractions Worksheets without diagrams
- Comparing Fractions Riddles
- More related Math resources
- Comparing Fractions Online Quiz
Comparing Fractions Worksheets
How to Compare Fractions
We can compare fractions using different ways.
- using diagrams - this is a supported, easier way;
- using knowledge of converting fractions to the same denominators which is harder.
One thing to remember is that if we are comparing two fractions without using diagrams, then it is much easier to do if they have the same denominator (or the same numerator).
Before you start comparing fractions, you should know about equivalent fractions.
Comparing fractions using diagrams Examples
Using diagrams can be a great way to help children understand about comparing fractions.
Also, if we are used to seeing fractions visually, this can really help us get an understanding of how much of a whole they represent.
You can see and compare how much of each diagram is shaded and see which fraction is bigger, or whether they are the same size.
Example 1) Compare \[ {3 \over 4} \; and \; {5 \over 6} \]
We can use diagrams to look at two fraction circles with the relevant fractions shaded.
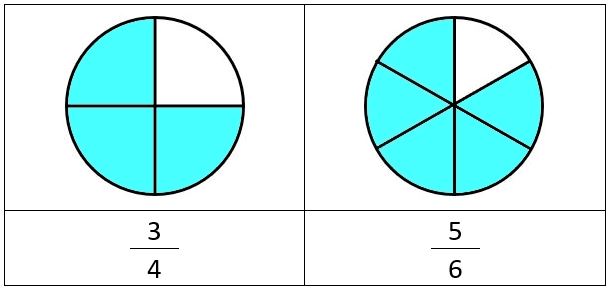
These diagrams clearly show that: \[ {3 \over 4} \] is the smaller of the two fractions as less of the diagram is shaded.
So we now know \[ {3 \over 4} \; < \; {5 \over 6} \]
Example 2) Let us compare \[ {2 \over 8} \; and \; {1 \over 4} \].
We can use diagrams to look at two fraction circles with the relevant fractions shaded.
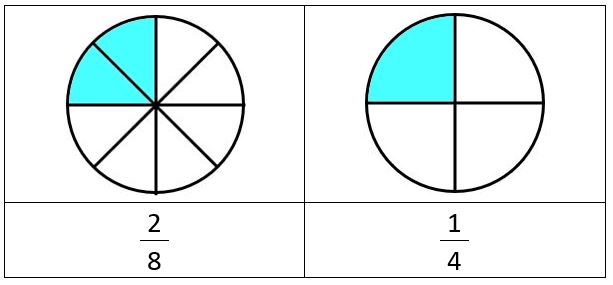
These diagrams show the same amount shaded for each fraction, so the two fractions are equal.
We have found out that \[ {2 \over 8} \; = \; {1 \over 4} \].
Comparing fractions without diagrams Examples
If there are no diagrams to help us, then we can use our knowledge of fractions to help us.
There are several examples given here which use different ways to compare the size of the fractions.
Example 1) Compare \[ {1 \over 2} \; and \; {3 \over 7} \]
If we are comparing a fraction with a half, it is usually quite quick and easy to tell whether it is bigger or not.
If a fraction is equivalent to a half, then the numerator is equal to half the denominator.
In this case, half of 7 = 3.5, so if the numerator was 3.5 the two fractions would be equal, or equivalent.
However, this numerator is equal to 3, which is smaller than 3.5, so the fraction is less than a half.
So this tells us \[ {1 \over 2} \; > \; {3 \over 7} \]
Example 2) Compare \[ {2 \over 5} \; and \; {3 \over 10} \]
We cannot directly compare these two fractions until their denominators are the same!
You will notice that in this case, one of the denominators is a multiple of the other: 10 is double 5.
So all we need to do is double the numerator and denominator of the first fraction to give us an equivalent fraction with the same denominator as the second fraction.
\[ {2 \over 5} = {2 \times 2 \over 5 \times 2} = {4 \over 10} \]
We can now compare the two fractions directly by looking at the numerators as the denominators are now the same.
4 is bigger than 3 so \[ {4 \over 10} \; > \; {3 \over 10}\]
So we have found out that \[ {2 \over 5} \; > \; {3 \over 10} \]
Example 3) Compare \[ {4 \over 9} \; and \; {3 \over 5} \]
These fractions are not multiples of each other but we can see that by comparing them each to a half, one is clearly bigger and the other is smaller.
If we look at \[ {4 \over 9} \] we can see that it is less than a half because the numerator is less than half of the denominator.
If we look at \[ {3 \over 5} \] we can see that it is more than a half because the numerator is greater than half of the denominator.
This tells us that \[ {4 \over 9} \; < \; {3 \over 5} \]
Example 4) Compare \[ {3 \over 7} \; and \; {3 \over 10} \]
You will notice that these fractions do not have the same denominator but they do have the same numerator.
This really helps us to compare them, because it means that if we think of fraction diagrams the circles have been split into different numbers of parts, but both fractions have the same number shaded in.
If we consider unit fractions, where the numerator is 1.
We know that: \[ {1 \over 7} \; > \; {1 \over 10} \] because the whole has been split into fewer pieces.
This tells us that \[ {3 \over 7} \; > \; {3 \over 10} \] because we are just shading in three pieces of each circle, and each of the sevenths is bigger than each of the tenths as the diagram below shows.
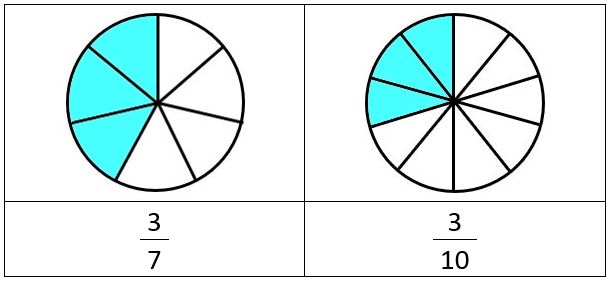
Example 5) Compare \[ {3 \over 7} \; and \; {2 \over 5} \]
If we look at both of these fractions, we can see (using the method above) that they are both smaller than a half.
We cannot directly compare these two fractions until their denominators are the same!
We now need to convert them both to fractions with the same denominator (or a common denominator) so we can compare them.
The best way to do this is to multiply the denominators together to tell us the denominator we need.
In this case 7 x 5 = 35, so we need a common denominator of 35.
To get a denominator of 35, we need to multiply the numerator and denominator of the first fraction by 5, and multiply the numerator and denominator of the 2nd fraction by 7.
This gives us: \[ {3 \over 7} \; = \; {3 \times 5 \over 7 \times 5} \; = \; {15 \over 35} \]
and \[ {2 \over 5} \; = \; {2 \times 7 \over 5 \times 7} \; = \; {14 \over 35} \]
Now that the fractions have the same denominator, we can compare the two numerators.
We can clearly see that \[ {15 \over 35} \; > \; {14 \over 35} \]
This tells us that: \[ {3 \over 7} \; > \; {2 \over 5} \]
Comparing Fractions Worksheets
Here you will find a selection of Fraction worksheets designed to help your child learn to compare and order fractions.
The sheets are carefully graded so that the easiest supported sheets come first, and the most difficult sheets come later on.
We have split the sheets into 5 sections with the first two section looking at comparing and ordering visual fractions using diagrams.
For the sheets in the third and fourth sections, children need to understand how to convert fractions to fractions with like denominators.
The 5th section is applying your knowledge and skills of comparing fractions to solving some comparing fraction riddles.
Using these sheets will help your child to:
- understand how to compare fractions using diagrams;
- practice comparing and ordering a range of fractions;
- use equivalence to compare two fractions.
These sheets are suitable for 4th and 5th graders.
Want to test yourself to see how well you have understood this skill?
- Try our NEW quick quiz at the bottom of this page.
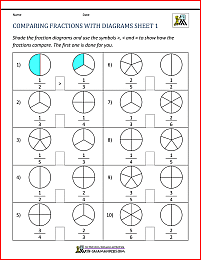
Section 1 - Comparing Fractions Worksheet with diagrams
These sheets are all about using fraction diagrams to compare two fractions.
Section 2 - Ordering Fractions Worksheet with diagrams
These sheets are similar to those in the section above, but you have to put 4 fractions in order from smallest to largest using diagrams for support.
Section 3 - Comparing Fractions Worksheet without diagrams
These sheets are all about using fraction knowledge and converting fractions to the same denominator to compare two fractions.
This first sheet just compares simple fractions with the same denominator or the same numerator, or equivalent to a half.



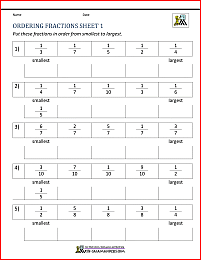
Section 4 - Ordering Fractions Worksheets without diagrams
These sheets are similar to those in the section above, but you have to put 5 fractions in order from smallest to largest.
Section 5 - Comparing Fractions Riddles
A great opportunity to test your fraction comparing skills and fraction knowledge to solve a range of fraction riddles!
More Recommended Math Worksheets
Take a look at some more of our worksheets similar to these.
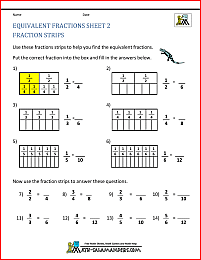
Equivalent Fractions
Equivalent fractions are fractions which have the same value as each other.
Before you can compare fractions, you should have a good understanding of what equivalent fractions are.
The printable fraction page below contains more support, examples and practice using equivalent fractions.
Simplifying Fractions
Take a look at our Simplifying Fractions Practice Zone or try our worksheets for finding the simplest form for a range of fractions.
You can choose from proper fractions, improper fractions or both.
You can print out your results or benchmark your scores against future achievements.
Good for practising equivalent fractions as well as converting to simplest form.
Great for using with a group of children as well as individually.
Least Common Multiple Calculator
Our Least Common Multiple Calculator will find the lowest common multiple of 2 or more numbers.
It will tell you the smallest multiple to convert the denominators of the fractions you are comaring into.
There are also some worked examples.
Learning Fractions
Are you looking for free fraction help or fraction support?
Here you will find a range of fraction help on a variety of fraction topics, from simplest form to converting fractions.
There are fraction videos, worked examples and practice fraction worksheets.
Improper Fractions
We have a support page to help students understand how what improper fractions are and how to conver them.
We also have a wide range of Improper Fraction Worksheets, some of which use visual fractions to aid understanding and some sheets which are more abstract.
Comparing Fractions Online Quiz
Our quizzes have been created using Google Forms.
At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.
This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.
For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.
We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.
We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.
For more information on the information we collect, please take a look at our Privacy Policy
We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.
This quick quiz tests your understanding and skill at comparing two or more fractions.
Fun Quiz Facts
- This quiz was attempted 771 times in the last academic year.
- The average (mean) score was 13.3 out of 20 marks.
- Can you beat the mean score?
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
Subscribe to Math Salamanders News
Sign up for our newsletter and get free math support delivered to your inbox each month. Free seasonal math grab pack included.
Return to 4th Grade Math Worksheets
Return from Comparing Fractions Worksheet to Math Salamanders Homepage
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.


















New! Comments
Have your say about the Math resources on this page! Leave me a comment in the box below.