- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- Donate
Rounding Numbers
Hub Page

Welcome to the Math Salamanders' Rounding Numbers hub page.
Here you will find links to a range of different rounding worksheets which will help your child to understand about rounding different numbers and quantities.
As well as a great selection of rounding number worksheets, we also have an online rounding zone where you can practice your skills online!
- This page contains links to other Math webpages where you will find a range of activities and resources.
- If you can't find what you are looking for, try searching the site using the Google search box at the top of each page.
Rounding Numbers
Are you needing to round numbers to the nearest 10,100 or 1000?
Need help rounding to 2dp?
Wanting to round to 3 significant figures and don't know how?
This page will help you understand all about rounding!
Quicklinks to ...
- Online Rounding Practice
- Rounding Worksheet Generator
- Rounding to the nearest 10
- Rounding to the nearest 100
- Rounding to the nearest 1,000
- Rounding Challenges to the nearest 10, 100 or 1,000
- Rounding to the nearest whole
- Rounding to 1dp
- Rounding to 2dp
- Rounding Decimals Challenges
- Rounding to Significant Figures
Online Rounding Practice Zone
In our Rounding Practice zone, you can practice rounding a range of numbers. You can round numbers to the nearest 10, 100 or even 1000. Want to round numbers to the nearest decimal place, you can do that too!
Select the numbers you want to practice with, and print out your results when you have finished.
You can also use the practice zone for benchmarking your performance, or using it with a group of children to gauge progress.
Rounding Off Worksheet Generator
Here is our generator for generating your own rounding off numbers worksheets.
Our generator will create the following worksheets:
- rounding off to the nearest 10, 100, 1000 or 10000
- rounding to the nearest whole, to 1dp, or 2dp.
- rounding off to 1sf, 2sf or 3sf
Rounding numbers to the nearest 10
When you are rounding a number to the nearest 10, you are trying to find out which multiple of 10 your number is closest to.
The golden rule with rounding is that if a number is exactly halfway between two multiples of 10, you always round up.
How to round a number to the nearest 10
Look at the ones digit.
- if it is less than 5 then round the number down by changing the ones digit to zero;
- if it is 5 or more then round the number up by adding one on to the tens digit and changing the ones digit to zero.
Examples
- 37 rounds up to 40 because the ones digit is 7.
- 63 rounds down to 60 because the ones digit is 3.
- 145 rounds up to 150 because the ones digit is a 5.
Rounding numbers to the nearest 100
When you are rounding a number to the nearest 100, you are trying to find out which multiple of 100 your number is closest to.
How to round a number to the nearest 100
Look at the tens digit.
- if it is less than 5 then round the number down by changing the tens digit and ones digit to zero;
- if it is 5 or more then round the number up by adding one on to the hundreds digit and changing the tens and ones digit to zero.
Examples
- 287 rounds up to 300 because the tens digit is 8.
- 1629 rounds down to 1600 because the tens digit is 2.
- 950 rounds up to 1000 because the tens digit is a 5.
Rounding numbers to the nearest 1000
When you are rounding a number to the nearest 1000, you are trying to find out which multiple of 1000 your number is closest to.
How to round a number to the nearest 1000
Look at the hundreds digit.
- if it is less than 5 then round the number down by changing the hundreds, tens and ones digits to zero;
- if it is 5 or more then round the number up by adding one on to the thousands digit and changing the hundreds, tens and ones digits to zero.
Examples
- 4687 rounds up to 5000 because the hundreds digit is 6.
- 8296 rounds down to 8000 because the hundreds digit is 2.
- 11583 rounds up to 12000 because the hundreds digit is a 5.
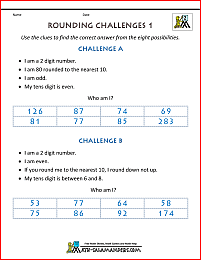
Rounding Challenges to the nearest 10, 100 or 1000
Here is our rounding challenges collection which will give your child an opportunity to apply their rounding learning.
The challenges can be tackled individually or with a partner.
Each challenge involves using rounding knowledge and properties of numbers to work out the correct answer.
Using these sheets will help your child to:
- apply their knowledge of rounding to the nearest 10, 100 or 1000;
- develop their problem solving skills;
- develop their understanding about place value and properties of numbers.
All the rounding challenges support elementary math benchmarks.
Rounding Decimals
When you are rounding decimals, you will either be rounding to the nearest whole number, or you will be rounding to a given number of decimal places or significant figures.
Help with each of these options and examples is given below.
Rounding to the nearest whole number
When you are rounding a number to the nearest whole number, you are trying to find out which whole number (or integer) your number is closest to.
How to round a number to the nearest integer (whole number)
Look at the tenths digit (the digit after the decimal point).
- if it is less than 5 then round the number down by removing the decimal part of the number;
- if it is 5 or more then round the number up by adding one on to the ones digit and removing the decimal part of the number.
Examples
- 3.8 rounds up to 4 because the tenths digit is an 8.
- 6.29 rounds down to 6 because the tenths digit is a 2.
- 12.527 rounds up to 13 because the tenths digit is a 5.
Rounding numbers to the nearest tenth (or one decimal place)
When you are rounding a number to the nearest tenth, you are trying to reduce your decimal to the closest decimal with just one decimal place.
How to round a number to the nearest tenth (or 1dp)
Look at the hundredths digit (the digit after the tenths digit).
- if it is less than 5 then round the number down by removing the decimal part of the number after then tenths digit;
- if it is 5 or more then round the number up by adding one on to the tenths digit and removing the rest of the decimal part of the number.
Examples
- 1.76 rounds up to 1.8 because the hundredths digit is a 6.
- 8.746 rounds down to 8.7 because the hundredths digit is a 4.
- 14.252 rounds up to 14.3 because the hundredths digit is a 5.
Rounding numbers to 2dp (or 2 decimal places)
When you are rounding a number to 2 decimal places, you are trying to reduce your decimal to the closest decimal with 2 decimal places.
How to round a number to 2dp (2 decimal places)
Look at the 3rd decimal digit (the digit after the hundredths digit).
- if it is less than 5 then round the number down by removing the decimal part of the number after the 2nd decimal place;
- if it is 5 or more then round the number up by adding one on to the hundredths digit and removing the rest of the decimal part of the number after this.
Examples
- 3.729 rounds up to 3.73 because the 3rd decimal digit is a 9.
- 18.1827 rounds down to 18.18 because the 3rd decimal digit is a 2.
- 27.625 rounds up to 27.63 because the 3rd decimal digit is a 5.
Rounding Decimals Challenges to the nearest whole, tenth or 2dp
Here is our rounding decimal challenges collection which will give your child an opportunity to apply their decimal rounding learning.
The challenges can be tackled individually or with a partner.
Each challenge involves using rounding knowledge and properties of numbers to work out the correct answer.
Using these sheets will help your child to:
- apply their knowledge of rounding to the nearest whole, tenth, or 2dp;
- develop their problem solving skills;
- develop their understanding about place value and properties of numbers.
All the rounding challenges support elementary math benchmarks.
Rounding numbers to Significant Figures
Rounding to significant figures is different from rounding to decimal places.
The first significant figure is the first non-zero digit a number has.
The second significant figure is the digit after the 1st significant figure.
The third significant figure is the digit after the 2nd significant figure, and so on.
See below for help to round a number to a set number of significant figures.
Rounding numbers to 1 significant figure (1SF)
When you are rounding a number to 1 significant figures, you are trying to reduce the number to a single digit and zeros (and possibly a decimal point) to indicate its place value.
How to round a number to 1 significant figure
Look at the 2nd significant digit that the number has.
In a decimal, the first significant digit is the first non-zero digit. The 2nd significant digit is the digit after the first.
- if it is less than 5 then round the number down by removing the rest of the number after the 1st significant digit and filling in with zeros;
- if it is 5 or more then round the number up by adding one on to the 1st digit and removing the rest of the number and filling in with zeros.
Examples
- 8726 rounds up to 9000, because the 2nd significant digit is a 7.
- 73.283 rounds down to 70 because the 2nd significant digit is a 3.
- 152 rounds up to 200 because the 2nd significant digit is a 5.
- 0.003826 rounds up to 0.004 because the 2nd significant digit is an 8.
- 0.60828 rounds down to 0.6 because the 2nd significant digit is a 0.
Rounding numbers to 2 significant figures (2sf)
When you are rounding a number to 2 significant figures, you are trying to reduce the number to a two digits and zeros (and possibly a decimal point) to indicate its place value.
How to round a number to 2 significant figures
Look at the 3rd significant digit that the number has.
This is the digit which is two digits after the most significant digit.
- if it is less than 5 then round the number down by removing the rest of the number after the 2nd significant digit and filling in with zeros;
- if it is 5 or more then round the number up by adding one on to the 2nd significant digit and removing the rest of the number and filling in with zeros.
Examples
- 5271 rounds up to 5300, because the 3rd significant digit is a 7.
- 73.483 rounds down to 73 because the 3rd significant digit is a 4.
- 175 rounds up to 180 because the 3rd significant digit is a 5.
- 0.003826 rounds down to 0.0038 because the 3rd significant digit is a 2.
- 0.60828 rounds up to 0.61 because the 3rd significant digit is an 8.
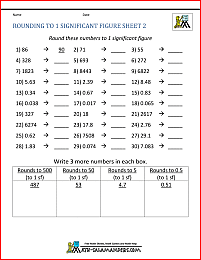
Rounding to 3 significant figures (3sf)
When you are rounding a number to 3 significant figures, you are trying to reduce the number to a 3 digits and zeros (and possibly a decimal point) to indicate its place value.
How to round a number to 3 significant figures
Look at the 4th significant digit that the number has.
- if it is less than 5 then round the number down by removing the rest of the number after the 3rd significant digit and filling in with zeros;
- if it is 5 or more then round the number up by adding one on to the 3rd significant digit and removing the rest of the number and filling in with zeros.
Examples
- 5261 rounds down to 5260, because the 4th significant digit is a 1.
- 73.285 rounds up to 73.3 because the 4th significant digit is an 8.
- 1805 rounds up to 1810 because the 4th significant digit is a 5.
- 0.003826 rounds up to 0.00383 because the 4th significant digit is a 6.
- 0.07284 rounds down to 0.0728 because the 4th significant digit is a 4.
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
Subscribe to Math Salamanders News
Sign up for our newsletter and get free math support delivered to your inbox each month. Free seasonal math grab pack included.
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.










New! Comments
Have your say about the Math resources on this page! Leave me a comment in the box below.