- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- Donate
List of Geometric Shapes
Welcome to the Math Salamanders' Geometric Shapes Information Page.
Here you will find a list of different geometric shapes to help you to identify a range of 2d and 3d shapes.
Along with each shape, we have also included the properties of each shape and other helpful information.
List of Geometric Shapes
Here you will find our list of different Geometric shapes.
There is a 2d shape area followed by a 3d shape area.
There is an image of each shape, as well as the properties that the shape has.
Using these sheets will help your child to:
- know the properties of different 2d & 3d shapes;
- recognise different 2d & 3d shapes;
- know the interior angles of regular polygons;
All the Math sheets in this section follow the Elementary Math Benchmarks.
Quicklinks to ...
2d Geometric Shapes
Here are our list of 2d geometric shapes, including triangles, quadrilaterals and polygons
List of Geometric Shapes - Triangles
|
Equilateral Triangle
|
Equilateral triangles have all angles equal to 60° and all sides equal length. All equilateral triangles have 3 lines of symmetry. |
|
Isoscles Triangle
|
Isosceles triangles have 2 angles equal and 2 sides of equal length. All isosceles triangles have a line of symmetry. |
|
Scalene Triangle
|
Scalene triangles have no angles equal, and no sides of equal length. |
|
Right Triangle
|
Right triangles (or right angled triangles) have one right angle (equal to 90° ). |
|
Obtuse Triangle
|
Obtuse triangles have one obtuse angle (an angle greater than 90° ). The other two angles are acute (less than 90° ). |
|
Acute Triangle
|
Acute triangles have all angles acute. |
Is an Equilateral triangle a special case of an Isosceles triangle?
According to Wikipedia:
" In geometry, an isosceles triangle is a triangle that has two sides of equal length. Sometimes it is specified as having two and only two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. "
Source: https://en.wikipedia.org/wiki/Isosceles_triangle
This means that there is some dispute as to whether an equilateral triangle is a special case of an isosceles triangle or not!
Most modern textbooks include use the 'at least' definition for isosceles triangles.
List of Geometric Shapes - Quadrilaterals
A quadrilateral is a polygon with 4 sides.
Quadrilaterals are also sometimes called quadrangles or tetragons.
There are quite a few members of the quadrilateral family.
There are also some members which are a subset of other members of this family!
See below if this confuses you!
|
Square
|
Squares have 4 equal sides and 4 right angles. They have 4 lines of symmetry. All squares belong to the rectangle family. All squares belong to the rhombus family. All squares are also parallelograms. |
|
Rectangle
|
Rectangles have 4 sides and 4 right angles. They all have 2 lines of symmetry (4 lines if they are also a square!) All rectangles belong to the parallelogram family. |
|
Rhombus
|
Rhombuses (rhombii) have 4 equal sides. Both pairs of opposite sides are parallel. They all have 2 lines of symmetry (4 lines if they are a square!) All rhombuses belong to the parallelogram family. |
|
Parallelogram
|
Parallelograms have 2 pairs of parallel sides. Some parallelograms have lines of symmetry (depending on whether they are also squares, rectangles or rhombuses), but most do not. |
|
Trapezoid US
|
Trapezoids US (Trapeziums UK) have one pair of parallel sides. Some trapezoids have a line of symmetry. Please note the differences between the definitions for US and UK. |
|
Kite
|
Kites have 2 pairs of equal sides which are adjacent to each other. |
|
Trapezium US
|
Trapeziums US (Trapezoids UK) are quadrilaterals with no parallel sides. Please note the differences between the definitions for US and UK. |
Convex and Concave Polygons
Polygons can be concave or convex in their shape.
Convex shapes have all angles less than 180°
Concave shapes have at least one reflex angle greater than 180°
Triangles are always convex.
|
Convex hexagon 
Convex shapes have no reflex angles (angles > 180° ) |
Concave hexagon 
Concave shapes have at least one reflex angle greater than 180° |
|
Convex pentagon 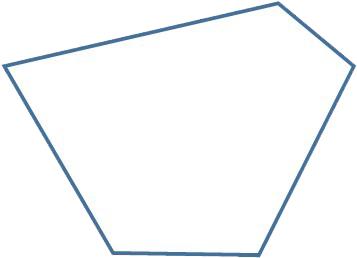
|
Concave pentagon 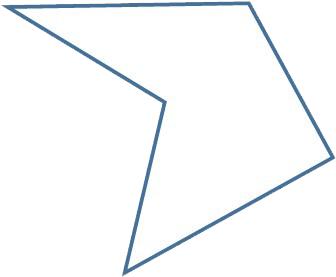
|
|
Convex octagon 
|
Concave octagon 
|
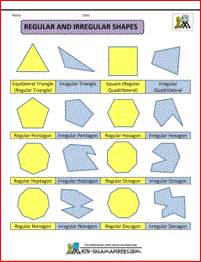
Regular and Irregular Polygons
Here is a list of regular polygons from 3 to 10 sides.
For each polygon, a regular and an irregular example have been shown.
Any regular shape will be mathematically similar to the example shown (having the same angles).
Regular shapes are always convex.
Irregular shapes can be concave or convex.
There are an infinite number of examples of different irregular polygons that could be shown, and only one example is given.
REGULAR SHAPES |
IRREGULAR SHAPES |
|
Equilateral Triangle 
Sides: 3 Angle: 60° Interior angles add up to 180° |
Irregular Triangle 
|
|
Square 
Sides: 4 Angle: 90° Interior angles add up to 360° |
Irregular Quadrilateral 
|
|
Pentagon 
Sides: 5 Angle: 108° Interior angles add up to 540° |
Irregular Pentagon
|
|
Hexagon 
Sides: 6 Angle: 120° Interior angles add up to 720° |
Irregular Hexagon 
|
|
Heptagon 
Sides: 7 Angle: 128.6° (to 1dp) Interior angles add up to 900° |
Irregular Heptagon 
|
|
Octagon 
Sides: 8 Angle: 135° Interior angles add up to 1080° |
Irregular Octagon 
|
|
Nonagon 
Sides: 9 Angle: 140° Interior angles add up to 1260° |
Irregular Nonagon 
|
|
Decagon 
Sides: 10 Angle: 144° Interior angles add up to 1440° |
Irregular Decagon 
|
|
Hendecagon 
Sides: 11 Angle: 147.3° (to 1dp) Interior angles add up to 1620° |
Irregular Hendecagon 
|
|
Dodecagon 
Sides: 12 Angle: 150° Interior angles add up to 1800° |
Irregular Dodecagon 
|
Formula for Interior Angles of a Polygon
The formulae for the interior angles of a polygon are as follows:
Total of interior angles = 180 x (number of sides - 2)
Interior Angle of a regular polygon = total of interior angles / number of sides
Example
What is the interior angle of a regular pentagon?
Step 1) Total of interior angles is 180 x (number of sides - 2)
= 180 x (5 - 2) = 180 x 3 = 540 °
Step 2) The interior angle = total of interior angles ÷ number of sides = 540 ÷ 5 = 108 °
Answer: 108 °
List of Geometric Shapes - Curved 2d Shapes
Here are some curved 2d shapes which have not yet been included.
|
Circle
|
Circles have a point in the centre from which each point on the diameter is equidistant. They have infinite lines of symmetry. How many sides does a circle have? This is an interesting question - the answer could be 0 (no straight sides), 1 curved side, or an infinite number of sides are all possible answers. |
|
Ellipse
|
Ellipses are like circles which have been squashed or stretched. They have 2 lines of symmetry. They are also a special type of oval. The longest and shortest diameters of the ellipse are called the major and minor axes. These axes are also the lines of symmetry. |
|
Crescent
|
Crescent shapes are made when two circles overlap, or when one circle is removed from another circle . The perimeter of crescents are made from two circular arcs. They have 1 line of symmetry. Our moon forms crescent shapes during its phases. Some countries such as Turkey or Algeria have crescent shapes on their flags. |
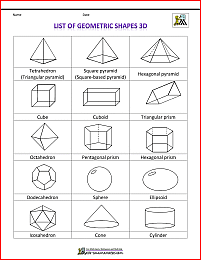
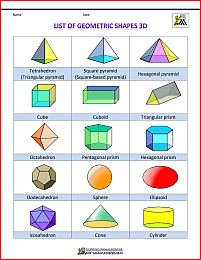
List of Geometrics Shapes - 3D Shapes
Here are some common 3D shapes that you should know.
Along with a picture of each shape, the number of faces, edges and vertices are also given.
Common properties of the 3D shapes are also given.
Please note that there is some disagreement over the definitions and properties of 3d shapes.
Some mathematicians allow a face to be curved and some do not.
Some mathematicians allow an edge to be curved and some do not.
|
Cube 
|
Cubes have 6 faces, 12 edges and 8 vertices. All sides on a cube are equal length. All faces are square in shape. A cube is a type of cuboid. |
|
Cuboid 
|
Cuboids have 6 faces, 12 edges and 8 vertices. All the faces on a cuboid are rectangular. |
|
Sphere 
|
Spheres have either 0 or 1 faces, 0 edges and 0 vertices. |
|
Ellipsoid 
|
Ellipsoids have either 0 or 1 faces, 0 edges and 0 vertices. |
|
Cylinder 
|
Cylinders have either 2 or 3 faces, 0 or 2 edges, and 0 vertices. |
|
Cone 
|
Cones have either 1 or 2 faces, 0 or 1 edges, and 1 apex (which is described by some mathematicians as a vertex). |
|
Triangular Prism 
|
Triangular Prisms have 5 faces, 9 edges, and 6 vertices. The two faces at either end are triangles, and the rest of the faces are rectangular. |
|
Hexagonal Prism 
|
Hexagonal Prisms have 8 faces, 18 edges, and 12 vertices. The two faces at either end are hexagons, and the rest of the faces are rectangular. |
|
Triangular-based Pyramid 
|
Triangular-based pyramids have 4 faces, 6 edges and 4 vertices. The base is a triangle. All of the faces are triangular. If the triangular faces making up the prism are all equilateral, then the shape is also called a Tetrahedron. |
|
Square-based Pyramid 
|
Square based pyramids have 5 faces, 8 edges and 5 vertices The base is a square. All the other faces are triangular. |
|
Hexagonal Pyramid 
|
Hexagonal pyramids have 7 faces, 12 edges, and 7 vertices. The base is a hexagon. All of the other faces are triangular. |
The 5 Platonic Solids
The platonic solids form a set of 5 polyhedra with the following special properties:
- the faces of the platonic solids have to be regular and congruent.
- the same number of faces meet at each vertex.
They are named after the Greek philosopher Plato who wrote about them in his philosophical discussions.
There are only 5 platonic solids:
- Regular tetrahedron
- Cube or regular hexahedron
- Regular octahedron
- Regular dodecahedron
- Regular icosahedron
|
Tetrahedron 
|
A Tetrahedrons is the same as a triangular pyramid. They have 4 triangular faces, 6 edges and 4 vertices. A regular tetrahedron has equilateral triangles for its faces, and is one of the 5 platonic solids. |
|
Cube (regular hexahedron) 
|
Cubes have 6 faces, 12 edges and 8 vertices. All sides on a cube are equal length. All faces are square in shape. A cube is a type of cuboid and is one of the 5 platonic solids. |
|
Octahedron 
|
Octahedrons are a shape with 8 faces, 12 edges and 6 vertices. A regular octahedron has equilateral triangles for its faces, and is one of the 5 platonic solids. |
|
Dodecahedron 
|
Dodecahedrons are a shape with 12 faces, 30 edges and 20 vertices. A regular dodecahedron has regular pentagons for its faces, and is one of the 5 platonic solids. |
|
Icosahedron 
|
Icosahedron are a shape with 20 faces, 30 edges and 12 vertices. All the faces are triangles. A regular icosahedron is one of the 5 platonic solids with all faces being equilateral triangles. |
Printable List of Geometric Shapes 2D
Here you will some printable 2d shape sheets showing a range of 2d shapes.
You can choose to have the properties of the 2d shapes displayed or not.
The sheets have been split up into US shapes and UK shapes, as there is a difference in the terminology used.

- List of 2D Geometric Shapes with properties
- PDF version
- List of 2D Geometric Shapes with properties (UK version)
- PDF version
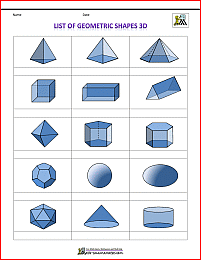
Printable Geometric Shapes 3D
Here you will some printable 3 d shape sheets showing a range of 3d shapes.
You can choose to have the sheet printed in color or black.
More Recommended Math Worksheets
Take a look at some more of our worksheets similar to these.
More Printable Shape Sheets - 2D & 3D Shape Sheets
Here you will find a selection of printable 2d and 3d shape sheets.
Each sheet is available in color or black and white, and labelled or unlabelled.
Using these sheets will help your child to:
- recognise and name a range of 2d and 3d shapes;
- recognise regular and irregular shapes.
Parts of a Circle Worksheets and Support
Do you know the special geometric names to describe the different parts of a circle?
Well you can find all the support you need on this page, complete with some practice worksheets and an online quiz!
Geometry Formula Sheet
Here you will find our support page about different Geometry formulas, including formulas about triangles, circles, quadrilaterals and polygons, as well as 3d shape formulae.
In the Geometry Cheat Sheet section you will find a range of printable geometry sheets with formula and information about angles, 2d and 3d shapes.
Using these sheets will help your child to:
- know different geometric formula;
- apply a range of formula to solve problems.
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
Subscribe to Math Salamanders News
Sign up for our newsletter and get free math support delivered to your inbox each month. Free seasonal math grab pack included.
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.
























New! Comments
Have your say about the Math resources on this page! Leave me a comment in the box below.