- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- Donate
Geometry Formula Sheet

Welcome to the Math Salamanders' Geometry Formula Sheet area.
Here you will find a range of different Geometry formulas for 2d and 3d shapes.
Geometry Formula Sheet
Here you will find our support page about different Geometry formulas, including triangles, circles, quadrilaterals and polygons, as well as 3d shapes.
Using these sheets will help your child to:
- know different geometric formula;
- apply a range of formula to solve problems.
Quicklinks to ...
Geometry Formula Sheet Angles
Angles in a triangle
|
Angles in a triangle add up to 180°\[ a + b + c = 180^o \] |
Angles on a straight line
|
Angles on a straight line add up to 180°\[ a + b = 180^o \] |
Angles around a point
|
Angles around a point add up to 360°\[ a + b + c + d + e = 360^o \] |
Convert Degrees to Radians
|
Convert from degrees (d) to radians (r)\[ r = {\pi \over 180 } d \] Convert from radians (r) to degrees (d)\[ d = {180 \over \pi } r \] Want to find out some more? |
Geometry Formulas Triangles
Angles in a triangle
|
Angles in a triangle add up to 180°\[ a + b + c = 180^{\circ } \] |
Area of a triangle
|
Area of a triangle\[ A = {1 \over 2} \times b \times h = { 1\over 2} bh \; or \; {bh \over 2} \] where b is the length of the base of the triangle and h is the perpendicular height. |
Pythagoras' Theorem
|
Pythagoras' theorem\[ a^2 + b^2 = c^2 \] where a,b and c are the sides of a right triangle. Side c is the hypotenuse (longest side). Pythagoras Theorem Worksheets |
Triangle Trigonometry - sine, cosine and tangent
|
Basic triangle trigonometry\[ sin (\theta) = {o \over h} \] \[ cos (\theta) = {a \over h} \] \[ tan (\theta) = {o \over a} \] |
The Sine and Cosine Rules
|
The Sine rule\[ {a \over sin(A)} = {b \over sin(B)} = {c \over sin(C)} \] The Cosine rule\[ a^2 = b^2 + c^2 - 2bc \cdot cos(A) \]
|
For more Geometry formulas about triangles, including examples showing the sine and cosine rules, use the link below.
Geometry Formula Sheet - Quadrilaterals
Angles in a quadrilateral
|
Angles in a quadrilateral add up to 360°\[ a + b + c + d = 360^o \] a + b + c + d = 360° |
Angles in a rectangle
|
Angles in a rectangle are all right angles (equal to 90°). |
Area and Perimeter of a rectangle
|
Area of a rectangle\[ A = a \times b \; or \; a \cdot b \] Perimeter of a rectangle\[ P = 2a + 2b \] where a and b are the lengths of the two adjacent sides. Want to know some more? |
Angles in a parallelogram
|
Angles in a parallelogramopposide angles are equal (opposite sides are also equal). \[ a + b = 180^o \] |
Area of a parallelogram
|
Area of a parallelogram\[ A = b \times h \] where b is the length of the base, and h is the perpendicular height of the parallelogram. Want to find out some more? |
Geometry Formula Sheet - Circles
Circumference of a circleThe circumference of a circle is the distance all the way around the outside of the circle, or the perimeter of the circle. |
The Circumference of a circle\[ C = 2 \pi r \; or \; \pi d \] where r is the radius of the circle and d is the diameter of the circle. Find out some more: |
Area of a circle
|
The area of a circle\[ A = \pi r^2 \] where r is the radius of the circle. Find out some more: |
Length of an arc of a circle
|
The length L of an arc of a circle is:\[ L = { \theta \over 180} \cdot \pi r \] where θ is the angle (in degrees) and r is the radius. |
|
Area of a sector of a circle
|
The area A of a sector of a circle is: \[ A = { \theta \over 360} \cdot \pi r^2 \] where θ is the angle (in degrees) and r is the radius. Want to find out some more? |
Triangle along a semicircle
|
A triangle drawn inside a circle with one side going along the diameter, and the other 2 sides meeting at any point along the edge of the circle will always make a right angle. The triangle will always be a right triangle. |
Geometry Formula Sheet - Regular Polygons
|
Equilateral Triangle
|
Angle: 60° Interior angles add up to 180° \[ Area = { \sqrt 3 \over 4} s^2 \] \[ Perimeter = 3s \] |
|
Square
|
Angle: 90° Interior angles add up to 360° \[ Area = s^2 \] \[ Perimeter = 4s \] |
|
Pentagon
|
Angle: 108° Interior angles add up to 540° \[ Area = {1 \over 4} s^2 \sqrt {5(5 + 2 \sqrt 5)} \] \[ Perimeter = 5s \] |
|
Hexagon
|
Angle: 120° Interior angles add up to 720° \[ Area = {3 \sqrt {3} \over 2} s^2 \] \[ Perimeter = 6s \] |
|
Heptagon
|
Angle: 128.6° (to 1dp) Interior angles add up to 900° \[ Area = {7 \over 4} s^2 \cot ({180^{\circ} \over 7}) \] \[ Perimeter = 7s \] |
|
Octagon
|
Angle: 135° Interior angles add up to 1080° \[ Area = 2 s^2 (1 + \sqrt 2) \] \[ Perimeter = 8s \] |
|
Nonagon
|
Angle: 140° Interior angles add up to 1260° \[ Area = {9 \over 4} s^2 \cot {20^{\circ}} \] \[ Perimeter = 9s \] |
|
Decagon
|
Angle: 144° Interior angles add up to 1440° \[ Area = {5 \over 2} s^2 \sqrt {5 + 2 \sqrt 5} \] \[ Perimeter = 10s \] |
Angles in a Regular Polygon
A general formula for this rule for an n-sided regular polygon is:
Interior angles add up to \[ (n - 2) \times 180^{\circ} \]
Each angle must be \[ {180 (n-2)^{\circ} \over n} \]
Area of a Regular Polygon
A general formula for the area of a regular polygon with n-side of length s is:
\[ A = {ns^2 \over 4 \tan ({180^{\circ} \over n})} \]
This can also be written: \[ A = {n \over 4 } s^2 \cot ({180 \over n})^{\circ} \]
For more support finding the area of regaular polygons, try our calculator:
Perimeter of a Regular Polygon
A general formula for the perimeter of a regular polygon with n-side of length s is:
\[ P = n \times s \]
Geometry Formula Sheet - 3D Shapes
|
Cubes
|
Volume of a cube:\[ V = a \times a \times a = a^3 \] Surface area of a cube:\[ A = 6a^2 \] where a is the length of each side. Want to find out some more? |
|
Cuboid
|
Volume of a cuboid:\[ V = l \times w \times h = lwh \] Surface area of a cuboid:\[ A = 2lw + 2wh + 2lh \] where l is the length, w is the width and h is the height of the cuboid. Looking for some more information? |
|
Sphere
|
Volume of a sphere:\[ V = {4 \over 3} \pi r^3 \] Surface area of a sphere:\[ A = 4 \pi r^2 \] where r is the radius of the sphere. Want some more information? |
|
Cylinder
|
Volume of a cylinder\[ V = \pi r^2 h \] Surface area of a closed cylinder:\[ A = 2 \pi r h + 2 \pi r^2 = 2 \pi r (r + h) \] Surface area of an open cylinder (a hollow tube):\[ A = 2 \pi r h \] where r is the radius of the cylinder and h is the height. Looking for more information? |
|
Cone
|
Volume of a cone\[ V = {1 \over 3} \pi r^2 h \] Surface area of a cone (including base):\[ A = \pi r^2 + \pi r s = \pi r (r + s) \] OR \[ A = \pi r (r + \sqrt {r^2 + h^2}) \] Surface area of a cone (excluding base):\[ A = \pi r s \] OR \[ A = \pi r \sqrt {r^2 + h^2} \] where r is the radius of the widest part of the cone, h is the height and s is the slant height of the cone. Want some more help? |
|
Square Pyramid
|
Volume of a square pyramid\[ V = {1 \over 3} b^2 h \] Surface area of a square pyramid (including base):\[ A = b^2 + 2 b s \] Surface area of a square pyramid (excluding base):\[ A = 2 b s \] where b is the length of one side of the base, h is the vertical height of the pyramid and s is the slant height of one of the triangles. Looking for more support? |
Pyramid (general)
|
Volume of any pyramid\[ {1 \over 3} A h \] where A is the area of the base, and h is the height. This formula works for any pyramid with a rectangular or triangular base and triangular sides. |
More Recommended Math Worksheets
Take a look at some more of our worksheets similar to these.
Geometry Cheat Sheets
Here you will find a range of geometry cheat sheets to help you answer a range of geometry questions.
The sheets contain information about angles, types and properties of 2d and 3d shapes, and also common formulas associated with 2d and 3d shapes.
Included in this page are:
- images of common 2d and 3d shapes;
- properties of 2d and 3d shapes;
- formulas involving 2d shapes, such as area and perimeter, pythagoras' theorem, trigonometry laws, etc;
- formulas involving 3d shapes about volume and surface area.
Using the sheets in this section will help you understand and answer a range of geometry questions.
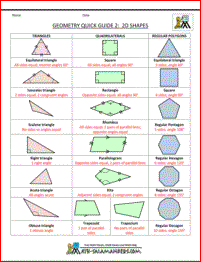
List of Geometric Shapes
Here you will find a List of different Geometric Shapes.
Included with each shape is a small picture and a description of the properties the shape has and how it relates to other shapes.
Included in this page are the following shapes:
- triangles
- quadrilaterals
- regular polygons
- irregular polygons
- a range of 3d shapes
All the printable Geometry worksheets in this section support the Elementary Math Benchmarks.
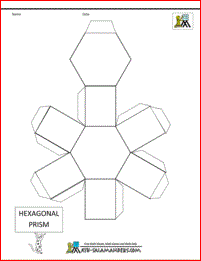
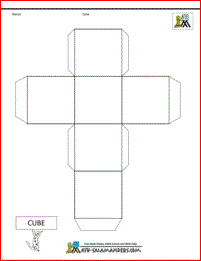
3D Geometric Shapes - Nets
Here you will find our range of Free Nets for 3D Shapes.
The following printables contain nets of common 3D shapes that your child should know. Each net sheet is available both with and without tabs to aid sticking together.
Using these sheets will help your child to:
- know the properties of different 3d shapes;
- recognise different 2d shapes inside the 3d shapes;
- construct a 3d shape from a net;
- recognise 3d shapes in different orientations and sizes;
- experience the fun and wonder of creating a 3d shape from a net.
Parts of a Circle Worksheets and Support
Do you know the special geometric names to describe the different parts of a circle?
Well you can find all the support you need on this page, complete with some practice worksheets and an online quiz!
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
Subscribe to Math Salamanders News
Sign up for our newsletter and get free math support delivered to your inbox each month. Free seasonal math grab pack included.
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.




































New! Comments
Have your say about the Math resources on this page! Leave me a comment in the box below.