- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- Donate
Volume of a Sphere Calculator

Welcome to our Volume of a Sphere Calculator page.
We explain how to find the volume of a sphere and provide a quick calculator to work it out for you, step-by-step.
There is also a separate calculator which will find the radius and diameter of a sphere, if you already know the volume.
Quicklinks to ...
Volume of a Sphere Calculators
We have two separate calculators for the volume of a sphere.
Our first calculator will take a measurement for the radius or diameter of the sphere and find the volume.
Our second calculator will take the volume and find the radius and diameter of the sphere.
Volume of a Sphere Calculator 1
This calculator finds the volume of a sphere when the radius or diameter is known.
How the Calculator Works
- Select if you want to use the radius or diameter (default is radius).
- For the value, you can choose a whole number, decimal or fraction.
- You can type a fraction by typing the numerator then '/' then the denominator.
- You can type a mixed number by typing the whole-number part, then a space then the fraction part.
- Examples: 2 1/2 (two and one-half); 3 4/5 (three and four-fifths); 7 1/3 (seven and one-third).
- Choose your units of measurement (default is cm)
- Choose your desired accuracy (default is 2 decimal places)
- Click the Find Volume button
- You will be given two answers for the volume, one in terms of Pi (π) and the other answer as a decimal value.
Volume of a Sphere Calculator 2
This calculator finds the radius and diameter of the sphere when the volume is known.
How the Calculator Works
- Choose the volume value: you can choose a whole number, decimal or fraction.
- Choose your units of measurement (default is none)
- Choose your desired accuracy (default is 2 decimal places)
- Click the Find Radius button
- You will be shown the radius and diameter of the sphere as a decimal to the required accuracy.
Volume of a Sphere Formula
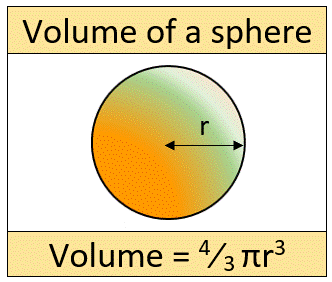
The formula for the volume of a sphere is: \[ V = {4 \over 3} \pi r^3 \] where V is the volume, and r is the radius of the sphere.
Volume of a Sphere Examples
Volume of a Sphere Example 1
Find the volume of the sphere below to 1 decimal place.

We can use Calculator 1 to solve this problem.
The formula for the volume of a sphere is: \[ V = {4 \over 3} \pi r^3 \]
If we substitute the values of the radius into this equation, we get: \[ V = {4 \over 3} \pi (8)^3 = {4 \over 3} \pi (512) = {2048 \over 3} \pi \]
This gives us a final answer of: \[ V = 2144.7 \;\ cm^3 \;\ to \;\ 1 \;\ decimal \;\ place \]
Volume of a Sphere Example 2
A large inflatable ball has a radius of 1 ½ meters. What is the volume of the ball? Give your answer to 2 decimal places.

We can use Calculator 1 to solve this problem.
The formula for the volume of a sphere is: \[ V = {4 \over 3} \pi r^3 \]
If we substitute the values of the radius into this equation, we get: \[ V = {4 \over 3} \pi (1 {1 \over 2})^3 = {4 \over 3} \pi ({27 \over 8}) = {9 \over 2} \pi \]
This gives us a final answer of: \[ V = 14.14 \;\ m^3 \; to \;\ 2 \;\ decimal \;\ places \]
Volume of a Sphere Example 3
A basketball has a diameter of 9.55 inches. What is the surface area of the ball? Give your answer to 1 decimal place.

We can use Calculator 1 to solve this problem, but we need to change the measurement from Radius to Diameter.
The first step is to find the radius of the ball.
The diameter of the ball is 9.55 inches. To find the radius, we have to halve the diameter (or divide the diameter by 2).
\[ 9.55 \div 2 = 4.775 \; inches \]
The formula for the volume of a sphere is: \[ V = {4 \over 3} \pi r^3 \]
If we substitute the values of the radius into this equation, we get: \[ V = {4 \over 3} \pi (4.775)^3 = {4 \over 3} \pi (108.87298...) = 145.16398... \pi \]
This gives us a final answer of: \[ V = 456.0 \;\ in^3 \; to \; 1 \; decimal \; place \]
Volume of a Sphere Example 4
A ball has a surface area of 500 square cm. What is the diameter of the ball? Give your answer to 1 decimal place.

In this case, we know the volume of the ball, but we need to find the diameter.
We can use Calculator 2 to solve this problem.
The formula for the volume of a sphere is: \[ V = {4 \over 3} \pi r^3 \]
This means that: \[ r^3 = V \div ({4 \over 3} \pi) = V \times {3 \over 4 \pi } = { 3V \over 4 \pi } \]
This means that the radius \[ r = \sqrt [\raise{7pt} \Large 3] ({ 3V \over 4 \pi}) \]
If we substitute the values of the surface area into this equation, we get: \[ r = \sqrt [\raise{7pt} \Large 3] ({ 3 \times 500 \over 4 \pi}) = \sqrt [\raise{7pt} \Large 3] ({ 1500 \over 4 \pi}) \]
This means that: \[ r = \sqrt[3] (119.3662...) \]
So if we work out the cube root: \[ r ≈ 4.924 \; cm \]
The diameter is equal to twice the radius.
This gives us a final answer of: \[ diameter = 4.924 \times 2 = 9.8 \; cm \; to \; 1 \; decimal \; place. \]
Volume of a Sphere Worksheets
We have created two worksheets to help you practice this skill.
The first sheet involves working out the volume of a range of spheres where the radius is given.
The second sheet involves working out the volume of spheres where the radius or diameter are given.
More Recommended Math Worksheets
Take a look at some more of our worksheets similar to these.
More Volume Worksheets
Here is our range of volume worksheets.
Using these sheets will help your child to:
- know what volume is and how to find it;
- find the volume of simple shapes by counting cubes;
- find the volume of rectangular prisms (cuboids);
- solving basic problems involving volume
More Area & Volume Calculators
We have a range of area and volume calculators to help you find the area and volumes of a range of different 2d and 3d shapes.
Each calculator page comes with worked examples, formulas and practice worksheets.
More Circle Worksheets and Support Pages
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
Subscribe to Math Salamanders News
Sign up for our newsletter and get free math support delivered to your inbox each month. Free seasonal math grab pack included.
Return to Calculators Hub page
Return from Volume of a Sphere Calculator to Math Salamanders Homepage
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.









New! Comments
Have your say about the Math resources on this page! Leave me a comment in the box below.