Square Inside a Circle Area
Support Page

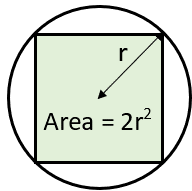
This page is all about how to find the area of a square whose sides are all touching the edge of a circle, as shown below.

We can use the information on this page to find the area of the square inside the circle (shaded green - as in Examples A and C).

We can also use the information to find the area of the circle that is outside of the square by subtracting the area of the square from the area of the circle (as in example B).

On this webpage you will find a range of support, examples and practice worksheets to help your child learn to work out the area of a square within a circle, or the left-over area of a circle outside a square (Example B).

There is also help if you know the area of the square but need to find the radius of the circle.

A square inside a circle (as shown) is sometimes called a square inscribed by a circle.

Our Square Inside a Circle Area sheets are graded from easiest to hardest, and each sheet comes complete with answers.

For those of you who like to know how things work, and why the formula is 2r², we will show you how it can be found below!

Let's start by looking at the four corners of the square and draw in one of the diagonals.

You will notice that the diagonal of the square is also the diameter of the circle as the diagonal goes from one side of the circle to the other through the center.

This means that the length of the diagonal is 2r, where r is the radius of the circle.

You can also see that the diagonal and two sides of the square into two right triangles.

Let's look closely at the right triangle that has been made by the diagonal of the square:

As the triangle is a right triangle, we can use Pythagoras' theorem to find the missing side s.

Pythagoras' theorem states that the sum of the squares of the two smaller sides of the triangle is equal to the square of the hypotenuse (which in this case is equal to 2r).

Writing this as an algebraic equation gives us: \[ s^2 + s^2 = (2r)^2 \]

This gives us \[ 2s^2 = 2r \cdot 2r = 4r^2 \]

So \[ s^2 = 2r^2 \]

We can simplify this to \[ s = \sqrt {2r^2} = \sqrt{2} r \]

As s is the vaue for the side of the square, this gives us:

The area of the square can now simply be found by multiplying two adjacent sides together to give:

\[ \sqrt{2} r \cdot \sqrt{2} r = \sqrt{2} \cdot \sqrt{2} \cdot r \cdot r = 2r^2 \]

So the Area of the Square Inside the Circle is \[ A = 2r^2 \]

We can also say that the perimeter of the square inside the circle is: \[ P = 4 \cdot (\sqrt{2} r) = 4 \sqrt{2} r \]

This is because the perimeter of the square is 4 multiplied by the side length.

If we already know the area of the square inscribed by the circle then we can find the radius of the circle using the formula below.

We can easily derive this formula since we know the area of the square (A) inside the circle is equal to double the square of the radius (r). \[ A = 2r^2 \]

If we make r the subject of this equation, then: \[ 2r^2 = A \]

So \[ r^2 = {A \over 2} \]

This gives us the radius of the circle
\[ r = \sqrt {A \over 2} \]

where r is the radius of the circle and A is the area of the square.

If you want to see how this works in practice, take a look at examples 4) and 5) below.

Area of a Square Inside a Circle Example 1

Find the area of the square below.

To find the area of the square we need to find the area A, where r=4cm. \[ A = 2r^2 \]

So \[ A = 2 \times 4^2 = 2 \times 4 \times 4 = 32 \]

So the area of the square is 32 cm².

Area of a Square Inside a Circle Example 2

Find the area of the square below.

In this case, the diameter of the circle is known, which is equal to twice the value of the radius.

So \[ r = 12 \div 2 = 6 \; inches\]

To find the area of the square we need to find the area A, where r = 6 inches. \[ A = 2r^2 \]

\[ So \; A = 2 \times 6 \times 6 = 2 \times 36 = 72 \]

So the area of the square is 72 in².

Area of a Square Inside a Circle Example 3

Find the area of the shaded parts of the circle that are outside square below. Give your answer to 1dp.

In this case, the we need to find the area of the parts of the circle that are outside of the square.

To do this we need to find the area of the square and subtract it from the area of the circle.

To find the area of the square we need to find the area A, where r = 7 cm. \[ A = 2r^2 \]

\[ So \; A = 2 \times 7^2 = 2 \times 7 \times 7 = 2 \times 49 = 98 \]

So the area of the square is 98 cm².

Next we will find the area of the whole circle.

The area of the circle is: \[ A = \pi r^2 = \pi 7^2 = \pi \times 7 \times 7 = 49 \pi = 153.9 cm \; to \; 1 \; decimal \; place \]

So we need to subtract the area of the square from the area of the whole circle.

\[ Area \; of \; shaded \; part \; = 153.9 - 98 = 55.9 \; cm^2 \]

So the area of the parts of the circle outside the square = 55.9 cm² to 1 decimal place

Area of a Square Inside a Circle Example 4

Find the diameter of the circle below, when the area of the square is 162 cm².

In this case, we know the area of the square, but we need to find the diameter of the circle.

We can use the formula \[ r = \sqrt {A \over 2} \] where r is the radius of the circle and A is the area of the square.

Substituting the value of the area of the square into this equation gives us: \[ r = \sqrt {162 \over 2} = \sqrt {81} = 9 \; cm \]

Now we have found the radius of the circle, we just need to double it to give us the diameter.

So the diameter of the circle is 9 x 2 = 18 cm.

Area of a Square Inside a Circle Example 5

Find the radius of the circle below, when the area of the square is 100 square inches. Give your answer to 1 decimal place.

In this case, we know the area of the square, but we need to find the radius of the circle.

We can use the formula \[ r = \sqrt {A \over 2} \] where r is the radius of the circle and A is the area of the square.

Substituting the value of the area of the square into this equation gives us: \[ r = \sqrt {100 \over 2} = \sqrt {50} = 7.071 \; in \]

So the radius of the circle is 7.1 inches to 1 decimal place.

For more help and support using Pythagoras' theorem, including how it works and some worked examples, take a look at our page below.

We have a range of other area worksheets and support pages for a range of different 2d shapes.

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.