- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- Donate
Factorising Quadratic Equations
Support Page

Welcome to the Math Salamanders' Factorising Quadratic Equations Support Page.
Here you will find help and support to enable you to
learn to factorise a range of different quadratic equations of the form ax2 + bx + c = 0.
All the quadratic equations in this section factorise into integer solutions inside each bracket.
Factorising Quadratic Equations Support
Factoring Quadratic Equation Worksheets
Definition of a Quadratic Equation
A quadratic equation is an equation involving the square of a number which is the highest power in the equation.
It is usually in the standard form:
ax2 + bx + c = 0
where a, b and c are numbers, and x is an unknown. The variable a cannot be 0 (but b and c can be 0)
Note that the operations can be '+' or '-'.
It is also sometimes called a second degree polynomial equation.
Examples
The following ARE quadratic equations in standard form:
- x2 + 7x + 4 = 0
- z2 - 25 = 0
- 2w2 + 7w = 0
- 2y2 - 28 = 0
- 4a 2 - ½ a + 15 = 0
The following ARE quadratic equations but not yet in standard form:
-
x2 + 6x = 4
- can be rewritten as x2 + 6x - 4 = 0 (which is in standard form)
-
3n2 - 10 = 6n
- can be rewritten as 3n2 - 6n - 10 = 0 (which is in standard form)
The following are NOT quadratic equations:
- x3 + 7x + 4 = 0 (because of the x3)
- 2y - 28 = 0 (because there is no y2 term)
- 4a5 - ½ a + 15 = 0 (because a has been raised to the 5th power)
How to solve a quadratic equation
There are 2 main methods to use when solving a quadratic equation:
1) The factoring method - this is used for paticular cases when the solution involves integers or fractions
2) The formula method - this can be used for any quadratic equation
Factorising Quadratic equations Support
Please note that this method will only work for specific cases of a quadratic equation with integer/fraction answers.
Take a general quadratic equation ax2 + bx + c = 0
Case 1) Is c=0?
If your quadratic equation just has x2 and x values, then we can simply use x as a common factor.
Example 1: 6x2 + 4x = 0
x is a common factor, so we can factorise this equation.
x(6x + 4) = 0
Now, we know that if two numbers multiply to give zero, then one of the numbers has to be equal to zero.
This means that either x = 0 or 6x + 4 = 0, in which case 6x=-4 so x=-4/6 or -2/3
Solutions: x=0 or x=-2/3
Example 2: 3x2 - 7x = 0
x is a common factor, so we can factorise this equation.
x(3x - 7) = 0
This means that either x=0 or 3x - 7 = 0
Solutions: x=0 or x=7/3
Case 2) Is a=1?
In simpler cases, the value of a=1 and you have x2 + bx + c = 0
Find two integers which multiply together to make c, but add together to give b.
This gives you the solutions for your two brackets, and hence the answer to the equation.
Example 1: x2 + 6x + 5= 0
In this example, we only have one x2 so a=1.
We can see that the c=5 and the factors of 5 are only 1 and 5 (as it is prime).
We also know that 1+5=6 so we have found our two numbers to go inside the brackets.
We end up with (x+1)(x+6)=0
This means that either x+1=0 (so x=-1) or x+6=0 (so x=-6).
Solutions: x=-1 or -6
Example 2: x2 -2x - 8 = 0
We can see in this example that a=1, b=-2 and c=-8
The factors of -8 are:
- 1 and -8
- -1 and 8
- 2 and -4
- -2 and 4
Looking at these factors, the pair of factors that add up to give b (which is -2) are 2 and -4.
We end up with (x + 2)(x - 4) = 0
This means that either x+2=0 (so x=-2) or x-4=0 (so x=4)
Solutions: x=-2 or 4
Example 3: x2 -7x + 10 = 0
We can see in this example that a=1, b=-7 and c=10
As c is positive, but b is negative, there must be 2 negative factors involved.
The (negative) factors of 10 are:
- -1 and -10
- -2 and -5
Looking at these factors, the pair of factors that add up to give b (which is -7) are -2 and -5.
We end up with (x-2)(x-5)=0
Solutions: x=2 or 5
Case 3) a is an integer >1.
This is quite tricky, so it is best to go through it with a worked example!
Example 1:
Find the solution of 2x2 - x - 6 = 0
Step i) Multiply a and c together.
This gives us 2x(-6)=-12
Step ii) Write down pairs of factors of a x c
Pairs of factors of -12 are:
- 1 and -12
- -1 and 12
- 2 and -6
- -2 and 6
- 3 and -4
- -3 and 4
Step iii) Look for a pair of factors which add up to make b.
The only pair of factors that add up to make -1 is 3 and -4.
Step iv) Rewrite the equation using this information to split up the x values
2x2 -x -6 = 2x2 + 3x - 4x - 6
Step v) Now factorise this expression in 2 parts with common factors
2x2 + 3x - 4x - 6 = x(2x + 3) - 2(2x + 3)
This gives us: (x-2) (2x + 3) or (2x + 3)(x - 2)
Solutions x=-3/2 or 2
Example 2:
Let's try 3x2 - 10x + 8 = 0
i) Multiply a and c together. This gives 3 x 8 = 24
ii) Write down pairs of factors of 24.
As b is negative, we are looking for 2 negative factors.
- -1 and -24
- -2 and -12
- -3 and -8
- -4 and -6
iii) Look for pairs of factors that add up to make b
The only two factors that add up to make -10 are -4 and -6.
iv) Rewrite the equation
3x2 - 10x + 8 = 3x2 - 4x - 6x + 8
v) Factorise this expression with common factors
3x2 - 4x - 6x + 8 = x(3x - 4) - 2(3x - 4)
This gives us: (x - 2)(3x - 4) or (3x - 4)(x - 2)
Solution: x = 4/3 or 2
Example 3:
Find the solutions to 2x2 - 9x - 5 = 0
i) Multiply a and c together. This gives us 2 x -5 = -10
ii) Write down the pairs of factors of -10.
Factors of negative 10 are:
- 1 and -10
- -1 and 10
- 2 and -5
- -2 and 5
iii) Look for the pair of factors that add up to make b.
The only two factors that add up to make b (which is -9) are 1 and -10.
iv) Rewrite the equation
2x2 - 9x - 5 = 2x2 -10x + x - 5
v) Factorise this expression
2x2 -10x + x - 5 = 2x(x - 5) + (x - 5)
This gives us (2x + 1)(x - 5)
Solutions: x = -1/2 or x = 5
Checking a Solution
One of the best and simplest things to do once you have solved a quadratic equation is to check your answers are correct.
All you need to do is to substitute the values of x into the equation and see if you are right!
If your answer does not work, try going through the steps again to see where you went wrong.
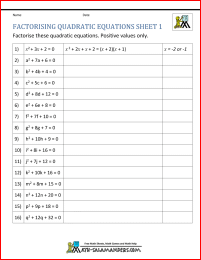
Factorising Quadratic Equation Worksheets
The sheets are arranged in order of difficulty to help introduce you into more complicated examples gradually.
Using these sheets will hopefully make factorising quadratic equations simple and straightforward.
The sheets cater for simpler and more complex quadratic equations.
Feedback on our Factorising Quadratic Equations Support Page
We hope you have found the support on our Factorising Quadratic Equations page useful.
Please feel free to leave us a message or comment at the bottom of this page and tell us what you think.
Your feedback helps us to improve the content and quality of our site.
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
Subscribe to Math Salamanders News
Sign up for our newsletter and get free math support delivered to your inbox each month. Free seasonal math grab pack included.
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments
Have your say about the Math resources on this page! Leave me a comment in the box below.