- Home |
- About |
- Contact Us |
- Privacy |
- Newsletter |
- Shop |
- Donate
Ordering and Comparing Rational Numbers

Welcome to our Ordering and Comparing Rational Numbers page.
Here you will find our range of 6th Grade worksheets and support
which will help you learn to order and compare negative numbers, fractions and decimals.
Want to test yourself to see how well you have understood this skill?.
- Try our NEW quick quiz at the bottom of this page.
Ordering and Comparing Rational Numbers
Here you will find a range of worksheets to help you to compare and order rational numbers and position them on a number line.
Ordering a set of rational numbers can bring together many different skills, from using absolute value to comparing decimals or fractions and understanding negative numbers.
The sheets have been put in order of difficulty, with the easiest first.
Each problem sheet comes complete with an answer sheet.
We have split our sheets into 3 different sections:
- Comparing Rational Numbers
- Ordering Rational Numbers
- Positioning Rational Numbers
Using these sheets will help you to practice these skills:
- compare rational numbers using > , < and =
- order a set of 4 to 5 rational numbers
- position rational numbers on a number line
- convert improper fractions into mixed numbers
Quicklinks to ...
What is a Rational Number?
A rational number is a number that can be made by dividing one integer by another (non-zero) integer.
All rational numbers can be written in the form a/b , where a and b are both integers and b is not equal to zero.
All integers, fractions, repeating decimals and terminating decimals (which do not go on forever) are rational numbers.
These numbers are rational and can all be written in the form a/b:
- 2.7 (it can be written as 27/10)
- 160 (it can be written as 160/1)
- 0.361 (it can be written as 361/1000)
- 0.121212... = 0.12 (it can be written as 12/99)
- 4.8888888... = 4.8 (it can be written as 44/9)
- -3.25 (it can be written as -13/4)
These numbers are not rational and cannot be written in the form a/b:
- \[ \sqrt{2}, \; \pi, \; \sqrt{11}, \; \sin (12^{\circ}), \; \cos (127^{\circ}), \; { 2\pi \over 3} \]
How to Order Rational Numbers
There are a few different skills you need to be able to do to order a set of rational numbers:
You need to be able to:
- Order a set of negative numbers including decimals
- Understand absolute value
- Convert an improper fraction into a mixed number
- Order a set of fractions
Once you have these skills, you are ready to order your rational numbers!
How to Order a set of Rational Numbers
- Convert any improper fractions into mixed numbers
- Split the numbers into two groups: negative numbers and positive numbers - remember absolute values cannot be negative
- Put the negative numbers in order - from least to greatest - which means from the most negative to the least negative.
- Put the positive numbers in order from least to greatest.
- Put your two lists together: first the negative list, then the positive list (if you have the number 0, then this goes in between the negative list and the positive list.
Ordering Rational Numbers Examples
Example 1) Put the following rational numbers in order, smallest first:
\[ 3.25, \; -2, \; |-1 {1 \over 2} |, \; {3 \over 4}, \; -{7 \over 2} \]
Step 1) Convert any improper fractions into mixed numbers.
\[ {7 \over 2} = 3 {1 \over 2} \]
So \[ -{7 \over 2} = -3 {1 \over 2} \]
Step 2) Sort the numbers into 2 groups: negative and positive:
Negative numbers are:
- \[ -2, \; -3 {1 \over 2} \]
Positive numbers are:
- \[ 3.25, \; |-1 {1 \over 2}|, \; {3 \over 4} \]
Step 3) Order the negative numbers from least to greatest.
The number which is the most negative has the lowest value.
\[ Least \; to \; Greatest: \; -3 {1 \over 2}, \; -2 \]
Step 4) Put the positive numbers in order from least to greatest.
\[ |-1 {1 \over 2}| = 1 {1 \over 2} \]
\[ Least \; to \; Greatest: \; {3 \over 4}, \; |-1 {1 \over 2}|, \; 3.25 \]
Step 5) Put the two lists together:
\[ -3 {1 \over 2}, \; -2, \; {3 \over 4}, \; |-1 {1 \over 2}|, \; 3.25 \]
\[ The \; order \; is \; - {7 \over 2}, \; -2, \; {3 \over 4}, \; |-1 {1 \over 2}|, \; 3.25 \]
Example 2) Put the following rational numbers in order, smallest first:
\[ |-4|, \; {7 \over 4}, \; -0.5, \; |-1.8|, \; -1 {2 \over 3} \]
Step 1) Convert any improper fractions into mixed numbers.
\[ {7 \over 4} = 1 {3 \over 4} \]
Step 2) Sort the numbers into 2 groups: negative and positive:
Negative numbers are:
- \[-0.5, \; -1 {2 \over 3} \]
Positive numbers are:
- \[ |-4|, \; 1 {3 \over 4}, \; |-1.8| \]
Step 3) Order the negative numbers from least to greatest.
The number which is the most negative has the lowest value.
\[ Least \; to \; Greatest: \; -1 {2 \over 3}, \; -0.5 \]
Step 4) Put the positive numbers in order from least to greatest.
\[ 1 {3 \over 4} = 1.75 \; which \; is \; less \; than \; 1.8 \]
\[ Least \; to \; Greatest: \; 1 {3 \over 4}, \; |-1.8|, \; |-4| \]
Step 5) Put the two lists together:
\[ -1 {2 \over 3}, \; -0.5, \; 1 {3 \over 4}, \; |-1.8|, \; |-4| \]
\[ The \; order \; is \; -1 {2 \over 3}, \; -0.5, \; {7 \over 4}, \; |-1.8|, \; |-4| \]
Ordering and Comparing Rational Numbers Worksheets
These sheets are put in order of difficulty with the easiest sheet first.
The sheets have been split into 3 sections:
- Comparing Rational Numbers Worksheets
- Ordering Rational Numbers Worksheets
- Positioning Rational Numbers Worksheets
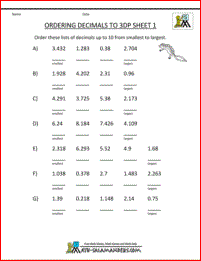
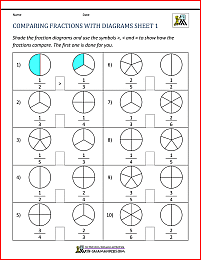
Comparing Rational Numbers Worksheets
Ordering Rational Numbers Worksheets
Positioning Rational Numbers Worksheets
More Recommended Math Worksheets
Take a look at some more of our worksheets similar to these.
Ordering Rational Numbers Skills Support
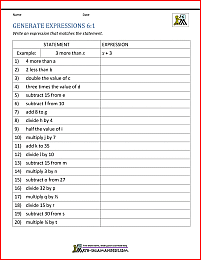
Expressions and Equations 6th Grade
The sheets on this page have been specially designed for 6th graders and are a great introduction to expressions and equations.
Inequalities
Ordering Rational Numbers Online Quiz
Our quizzes have been created using Google Forms.
At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.
This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.
For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.
We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.
We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.
For more information on the information we collect, please take a look at our Privacy Policy
We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.
This quiz tests your skill and apply your knowledge of ordering rational numbers here.
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
How to Print or Save these sheets 🖶
Need help with printing or saving?
Follow these 3 steps to get your worksheets printed perfectly!
Subscribe to Math Salamanders News
Sign up for our newsletter and get free math support delivered to your inbox each month. Free seasonal math grab pack included.
Return to 6th Grade Math Worksheets
Return from 6th Grade Order of Operations to Math Salamanders Homepage
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.













New! Comments
Have your say about the Math resources on this page! Leave me a comment in the box below.